   
|
|
|
|
A INVESTIGACIÓN CIENTÍFICA. O TRABALLO DE LABORATORIO. O INFORME DE LABORATORIO |
|
Desde o principio dos tempos tentamos como especie coñecer a contorna no que
nos moviamos e desenvolviamos a nosa vida. A curiosidade xogou un papel
fundamental, o descoñecido causábanos inquietude e temor ata que descubriamos
que non era perigoso para as nosas vidas. Os nosos antepasados desenvolveron
unha capacidade incrible para fabricar instrumentos, pensemos na talla de pedras
e o que iso supuxo para o principio da nosa especie. A observación, a
curiosidade, e ata a casualidade foron axudando a perfeccionar técnicas que logo
se transmitían e ensinaban de pais a fillos, nun principio do que sería a escola
e o ensino.
A medida que a filosofía nos ía dando unha explicación da nosa contorna, as
preguntas sobre o mundo que nos rodeaba fixéronse innumerables. Había cousas que
entendiamos, porque sempre sucedían da mesma forma, aínda que non soubésemos os
porqués. Cando non achabamos respostas adecuadas acudiamos á maxia,
superstición, ou relixión para dar sentido a todo. O mundo encheuse de deuses
caprichosos que eran responsables de todos eses fenómenos que non entendiamos e
preocupábannos.
Vexamos o seguinte capítulo de serie Cosmos, de Carl Sagan, titúlase a
harmonía dos mundos. Nel cóntanos as diferenzas da Astronomía e a Astroloxía,
que tentaban entender o funcionamento do Cosmos e a súa posible influencia sobre
as nosas vidas. Cóntanos tamén como descubrimos as leis que rexen o Universo.
Képler, como logo Galileo ou Newton, descobre as relacións matemáticas que fan
funcionar o Universo.
Sen as matemáticas, ou esas relacións sinxelas entre as magnitudes que
descubriamos coa observación, a ciencia non sería posible. E esta afianzouse ao
cimentarse no método científico, que como vimos o curso pasado permitíanos
comprobar as hipóteses verdadeiras das que non o eran.
Esta comprobación de hipótese realizámolas a través de experimentos ben
deseñados, controlando perfectamente as variables que interveñen, e realizados
as máis das veces nos laboratorios. Neles dispoñemos de aparellos e técnicas que
nos permiten controlar mellor as variables que interveñen nos fenómenos. Neles
obtemos os datos que mediante relacións matemáticas permítennos aceptar ou
refugar hipóteses. Estas relacións matemáticas serán a expresión máis elegante
das leis físicas que se agochan nos fenómenos naturais.
Pero nada disto sería útil se estes descubrimentos non se dan a coñecer a
toda a comunidade científica. Os informes de laboratorio pretenden deixar
constancia dos descubrimentos que facemos neles. Con eles permitiremos que eses
experimentos póidanse reproducir por outras persoas, dando máis validez aos
nosos decubrimientos.
As revistas científicas xogan un papel fundamental ao permitir compartir
coñecementos a toda a comunidade científica. O coñecemento enriquécenos a todos.
Pero para isto débese universalizar este compartir descubrimentos a través das
publicacións científicas. Sen elas sería impensable a rápida resposta a desafíos
tan grandes como supuxo esta pandemia de SARS- CoV-2, e o descubrimento en tan
pouco tempo de vacinas que nos permitan sobrepoñernos a esta enfermidade do
COVID-19.
Principais Revistas Científicas a Nivel Mundial
 |
 |
 |
 |
|
Le Journal des Savants, 1665,
primeira revista científica |
Philosophical Transactions, 1665,
publicada poa Royal Society |
Revista da Real Sociedade Española
de Química |
Chemistry — A European Journal |
 |
 |
 |
 |
|
Nature, dende 1869 |
Physical Review, da American
Physical Society |
Journal of the American Chemical
Society, publicada dende 1879 pola American Chemical Society |
The Lancet, revista médica
británica |

|
|
MAGNITUDES ESCALARES E VECTORIAIS |
|
Chamamos magnitudes ás propiedades da materia que se poden
cuantificar, é dicir, que se poden expresar con números. Hai propiedades que son
subxectivas, dependen de cada persoa, están relacionadas coas nosas sensacións,
por tanto non as podemos cuantificar. Por exemplo o sabor, unha substancia pode
ter un sabor picante, salgado ou amargo, por exemplo, pero non podemos
cuantificar a cantidade de proído ou amargura que nos produce esa substancia. O
que para un é picante para outro non o é, ou o é moito menos.
Outras propiedades como a masa, o tamaño, o tempo, si as podemos cuantificar,
expresar con números, entón podémolas chamar magnitudes.
As magnitudes sempre as expresaremos por unha cantidade numérica e unha
unidade, que será unha cantidade de magnitude que tomamos como referencia. Esta
cantidade, a unidade, escóllese por convenio, podemos elixir calquera cantidade
de magnitude, pero témonos que poñer de acordo para poder compartir datos das
medidas. Medir será comparar unha cantidade de magnitude con outra
cantidade de magnitude que chamamos unidade. Antigamente en Galicia as leiras
medíanse en ferrados, o ferrado dunha zona non era igual ao ferrado doutra, así
que as medidas só tiñan validez cando se referían a unha unidade que se
compartía e era coñecida.
As magnitudes teñen outra diferenza importante. Unhas quedan ben definidas
dando só o seu valor numérico e a unidade de medida, pero outras non. Cando
dicimos que a masa dun corpo é de 2 kg, queda ben definida a súa masa, non fai
falta dar máis información. Pero se dicimos que un corpo percorreu 5 m, ese
desprazamento non queda totalmente definido, fáltannos cousas por saber, por
exemplo cara a onde se desprazou 5 m.
As magnitudes que quedan ben definidas dando só o seu valor numérico e a
unidade chámanse magnitudes escalares.
As magnitudes das que hai que dar máis información que o seu valor numérico e
a unidade chámanse magnitudes vectoriais. Estas represéntanse por un
vector, que é un segmento orientado. Del debemos dar o seu módulo,
que será o valor numérico coa unidade, e represéntase pola lonxitude do
segmento; o punto de aplicación, que será a orixe do segmento; a
dirección que será a recta sobre a que está o segmento; e o sentido
que nolo dá unha punta de frecha que colocamos ao final do segmento.
Se representamos un desprazamento de 10 m cun vector, sabemos que o
desprazamento se realiza en dirección horizontal e cara á dereita, quedando así
perfectamente definido.
Son magnitudes escalares: a masa, a densidade, o volume, o tempo, por
exemplo.
Son magnitudes vectoriais: o desprazamento, a forza, a velocidade, a
aceleración, por exemplo. Estas representarémolas por vectores.
EXERCICIOS
PARA PRACTICAR

|
|
MAGNITUDES FUNDAMENTAIS E DERIVADAS. CAMBIO DE UNIDADES |
|
Ata finais
do século XIX, cada país utilizaba para medir una mesma magnitude unha unidade
diferente. Hoxe en día, a maioría dos países acepta o SISTEMA INTERNACIONAL
DE UNIDADES ( S.I.)
|
Magnitudes básicas do Sistema Internacional de Unidades |
|
MAGNITUDE |
UNIDADE |
SÍMBOLO |
| Lonxitude |
metro |
m |
| Masa |
quilogramo |
kg |
| Tempo |
segundo |
s |
| Intensidade de corrente eléctrica |
amperio |
A |
| Temperatura termodinámica |
grao Kelvin |
K |
| Cantidade de substancia |
mol |
mol |
| Intensidade luminosa |
candela |
cd |
|
DEFINICIÓNS |
| |
DEFINICIÓN
PREVIA |
DEFINICIÓN
DENDE 2019 |
| metro |
O metro é a distancia percorrida pola luz no baleiro
en
1/299.792.458 segundos. |
O metro, símbolo m, é a unidade SI de
lonxitude. Defínese ao fixar o valor numérico da velocidade da luz no
baleiro, c, en 299 792 458, cando se expresa na unidade m·s−1,
onde o segundo defínese en función da frecuencia do Cesio ΔνCs.
c = 299 792 458 m·s−1 |
| quilogramo |
Masa do quilogramo patrón internacional, que se
conserva en Sèvre, perto de Paris. |
O quilogramo, símbolo kg, é a unidade SI
de masa. Defínese ao fixar o valor numérico da constante de Planck, h, en
6,626 070 15·10−34, cando se expresa na unidade J· s, igual
a kg·m2·s−1, onde o metro e o segundo defínense
en función de c e ΔνCs. h = 6,626 070 15·10−34
J·s |
| segundo |
Duración de 9.192.631.770 períodos
da radiación do átomo de cesio-133 na transición entre dous niveis da estructura
hiperfina do seu estado fundamental. |
O segundo, símbolo s, é a unidade SI de
tempo. Defínese ao fixar o valor numérico da frecuencia da transición
hiperfina do estado fundamental non perturbado do átomo de cesio-133, ΔνCs,
en 9 192 631 770, cando se expresa na unidade Hz, igual a s−1.
ΔνCs = 9 192 631 770 s−1 |
| amperio |
Intensidade dunha corrente eléctrica constante que, cando flúe entre dous condutores paralelos de lonxitude indefinida e de sección transversal circular infinitamente pequena situados a unha distancia recíproca de 1 metro e colocados no baleiro, fai que un condutor exerza sobre o outro unha forza de
2.10-7 newtones por
cada metro. |
O amperio, símbolo A, é a unidade SI de
corrente eléctrica. Defínese ao fixar o valor numérico da carga elemental,
e, en 1,602 176 634 ·10−19, cando se expresa na unidade C, igual
a A· s, onde o segundo defínese en función de ΔνCs.
e = 1,602 176 634 ·10−19 C |
| kelvin |
Fracción 1/273,16 da temperatura termodinámica
do punto triple da auga. |
O kelvin, símbolo K, é a unidade SI de
temperatura termodinámica. Defínese ao fixar o valor numérico da constante
de Boltzmann, k, en 1,380 649 ·10−23, cando se expresa na unidade
J· K−1, igual a kg·m2·s−2·K−1,
onde o quilogramo, o metro e o segundo defínense en función de h, c e ΔνCs.
k = 1,380 649 ·10−23 J·K−1 |
| mol |
Cantidade de substancia dun sistema que
contén
tantas entidades elementais como átomos hai en 0,012 kg de carbono-12.
Débese especificar o tipo das entidades elementais, xa sexan átomos,
moléculas, ions, electróns, ou outras. |
O mol, símbolo mol, é a unidade SI de
cantidade de substancia. Un mol contén exactamente 6,022 140 76 ·1023
entidades elementais. Esta cifra é o valor numérico fixo da constante de
Avogadro, NA, cando se expresa na unidade mol−1, e
denomínase número de Avogadro.
A cantidade de substancia, símbolo n, dun sistema, é unha medida do número
de entidades elementais especificadas. Unha entidade elemental pode ser un
átomo, unha molécula, un ión, un electrón, calquera outra partícula ou grupo
especificado de partículas.
NA = 6,022 140 76 ·1023 entidades elementales. |
| candea |
Intensidade luminosa, nunha dirección dada, dunha fonte que emite unha radiación monocromática de frecuencia 540 × 1012 hercios e cuxa intensidade energética nesa dirección é 1/683 vatios por estereorradián. |
A candea, símbolo cd, é a unidade SI de
intensidade luminosa nunha dirección dada. Defínese ao fixar o valor
numérico da eficacia luminosa da radiación monocromática de frecuencia
540·1012 Hz, Kcd, en 683, cando se expresa na unidade
lm·W−1, igual a cd·sr·W−1, ou a cd· sr·kg−1·m−2·s3,
onde o quilogramo, o metro e o segundo defínense en función de h, c e ΔνCs.
Kcd = 683 lm·W−1 |
Para saber máis:
A revisión do sistema internacional de unidades, Estefanía de Mirandés, BIPM,
Centro Español de Metroloxía, 18 de Maio 2018
O
Sistema Internacional de Unidades, SI. Centro Español de Metroloxía, CEM
As unidades das magnitudes fundamentais defínense actualmente a
partir de fenómenos físicos, desligándoas dun patrón físico que se
gardaba nalgún lugar coñecido. Son así máis fáciles de reproducir en
calquera lugar do mundo. Para definilas establécese un valor fixo para
as constantes físicas a partir das que se definen.
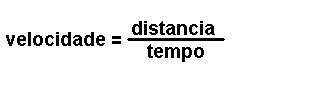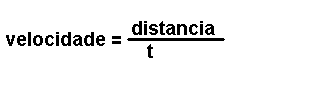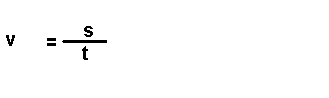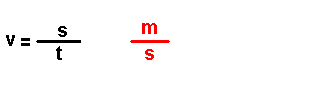
Son magnitudes que se definen a partir das magnitudes fundamentais. Por
exemplo:
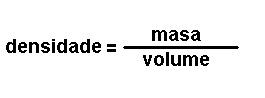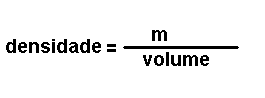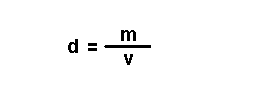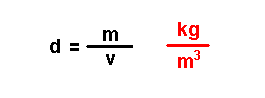
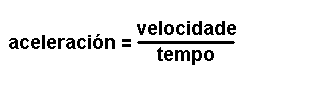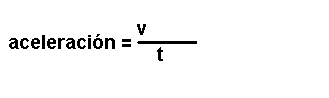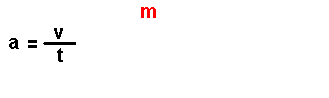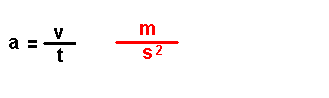
| Prefixo |
Símbolo |
Factor multiplicador |
| Tera- |
T |
1012 u |
| Xiga- |
G |
109 u |
| Mega- |
M |
106 u |
| quilo- |
k |
103 u |
| hecto- |
h |
102 u |
| deca- |
da |
10 u |
| unidade |
u |
1 u |
| deci- |
d |
10−1 u |
| centi- |
c |
10−2 u |
| mili- |
m |
10−3 u |
| micro- |
μ |
10−6 u |
| nano- |
n |
10−9 u |
| pico- |
p |
10−12 u |
O factor multiplicador é o número polo que tes que multiplicar a medida para
transformala na unidade.
Por exemplo, 2 Mm = 2·106 m ou
5 nm = 5·10-9 m
As unidades transfórmanse con facilidade a
través dos factores de conversión. Consiste en multiplicar unha medida
polo cociente que nos dá a equivalencia entre a unidade que queremos substituír
e a nova unidade. Este cociente ten valor unidade, xa que o numerador é
equivalente ao denominador. A unidade que poñemos no denominador é a que
queremos eliminar, e no numerador vai a nova unidade. Cando escribas a
equivalencia entre as unidades dálle valor unidade á maior delas. Por exemplo: é
máis fácil entender 1 km = 1000 m que 1 m = 0,001 km aínda que
sexan as dúas igualdades válidas.
A equivalencia entre (km) e (m) é: 1 km = 103 m

A equivalencia entre
(km) e (m) é: 1 km = 103 m. E a
equivalencia entre (h) e (s) é: 1 h
= 3600 s.

A equivalencia entre
(km) e (m) é: 1 km = 103 m. E a
equivalencia entre (h) e (s) é: 1 h
= 3600 s.

É importante tamén saber pasar de complexo de h: min: s a horas, e viceversa, xa
que na vida diaria manexámonos en horas, minutos e segundos. Por exemplo, cando
abriches esta páxina eran las:
. Que facer nestes casos?
Pasar de complexo a incomplexo: Cantas horas son 2 h:25 min:30 s?
a) Pasa os minutos a horas, e os segundos a horas e suma: 2 h:25 min:30 s = 2 h
+ 25 min · 1 h/60 min + 30 s · 1 h/3600 s = 2,425 h
b) Ou tamén, aproveitar a tecla (º ' '') de graos, minutos e segundos da
calculadora, que tamén segue o sistema sesaxesimal:
2 h:25 min:30 s = 2 (º ' '') 25 (º ' '') 30 (º ' '') = 2,425 h
Pasar de incomplexo a complexo: Cantas h: min: s son 1,755 h?
a) Pasa os decimais de horas a minutos, e os decimais de minutos a segundos:
1,755 h = 1 h + 0,755 h · 60 min/1 h = 1 h + 45,3 min = 1 h + 45 min + 0,3 min ·
60 s/1 min =1 h 45 min 18 s
b) Ou tamén, aproveitar a tecla (º ' '') de graos, minutos e segundos da
calculadora, que tamén segue o sistema sesaxesimal:
1,755 h = 1,755 (º ' '') (=) (º ' '') = 1º 45º 18 = 1 h 45 min 18 s
EXERCICIOS
PARA PRACTICAR

|
|
NOTACIÓN CIENTÍFICA. CIFRAS SIGNIFICATIVAS |
|
Cando temos que expresar cantidades moi grandes ou moi pequenas é moi útil
empregar un tipo de expresións que se denominan notación científica.
En que consiste? Consiste en escribir calquera número como produto dun
decimal e unha potencia de dez. O decimal debe ter só unha cifra antes da coma,
e esa cifra non pode ser cero. Pode haber potencias de expoñente positivo e
potencias de expoñente negativo, para valores inferiores á unidade.
Están ben escritos como notación científica os números:
2,5·102 3,45·1012
−6,03·10−2
1,002·10−3
Están mal escritos como notación científica os números:
0,5·104 23,87·105
−0,03·10−8 154,2·10−3
- Pasar un número a notación científica.
25475,45: Se o número é maior que 1, desprazamos a coma decimal cara á
esquerda ata a primeira cifra. Ao desprazala cara á esquerda, dividimos, entón
logo multiplicamos por dez elevado ao número de cifras sobre as que se desprazou
a coma. 2,547545·104
0,00057: Se o número é menor que 1, desprazamos a coma decimal ata
despois da primeira cifra distinta de cero. Ao desprazala cara á dereita,
multiplicamos, entón logo multiplicamos por dez elevado ao número de cifras
sobre as que se desprazou a coma con signo negativo. 5,7·10−4
Lembra que a potencia de expoñente negativo é o inverso da potencia de expoñente
positivo:
10−2 = 1/102
- Pasar de notación científica a número decimal.
3,985·105: Se o expoñente é positivo, desprazamos a coma cara
á dereita tantos lugares como indica o expoñente, completamos con ceros se é
necesario. 398500
2,0048·10−5:
Se o expoñente é negativo, desprazamos a coma cara á esquerda tantos lugares
como indica o expoñente. 0,000020048
- Comparar números en notación científica.
A notación científica é moi práctica para comparar números moi grandes ou moi
pequenos, bastará comparar o decimal se os expoñentes coinciden, e bastará
comparar os expoñentes se estes non coinciden.
2,5·102 < 4,5·102 < 8,25·102 < 6,4·103
< 1,15·105
EXERCICIOS
PARA PRACTICAR
- A notación científica na calculadora.
Como usar a notación científica nas calculadoras? Concretarei para o uso das
calculadoras CASIO, non por facerlle propaganda se non por ser as máis comúns
entre o meu alumnado.
 |
 |
| 123456789 x 386 = 4,765432055·1010 |
Cando unha operación dá un resultado que
ocupa máis díxitos que os que entran na pantalla a calculadora presenta o
resultado en notación científica. Aínda que a calculadora preséntao como =
4,765432055 10 Onde non aparece nin o punto do produto nin a base
10. |
 |
 |
| Hoxe en día xa hai modelos que inclúen o
signo do produto e a base 10 na pantalla, por iso é fundamental coñecer ben
a calculadora propia. Ah, un consello! Nunca pidas prestada unha calculadora
que non coñezas para facer un exame, sobre todo se é un exame importante. |
Se tes que introducir un número que estea
en notación científica: introduce o decimal, pulsa a tecla EXP e introduce o
expoñente. |
Un erro moi frecuente é introducir tamén o signo do
produto e a base 10, co que consegues multiplicar todo por dez. A tecla EXP o
que fai é introducir precisamente o signo do produto e a base 10, nós só temos
que introducir o decimal e o expoñente. Penso que precisamente o nome da tecla (
EXP) é o que leva a confusión, sería mellor que se denominase por exemplo
(·10x). Queda dito por se algún enxeñeiro de CASIO visita esta humilde
páxina, moitos alumnos agradeceríanlle o cambio.
 |
 |
| Se queres traballar sempre en
notación científica pódelo facer a través do modo SCI: pulsa a tecla MODE |
e logo o número
correspondente ao modo SCI, ás veces ese número hai que pulsalo varias
veces. Para saír do modo SCI pulsa modo NORM normal. |
Creo que hai alguén en CASIO que comparte as miñas ideas. Xa temos
calculadoras que cambiaron a tecla de ( EXP) pola tecla máis intuitiva de (·10x).
Os meus recoñecementos para CASIO, moitos estudantes vanllo a agradecer.
 |
 |
| Novos modelos de calculadora
sen a tecla de ( EXP) que tantos erros favorecía. Xa nos podemos
esquecer desta tecla que nos inducía a pensar só no expoñente. |
Acerto de CASIO corrixir esta
tecla que tantas dúbidas creaba. |
Cando realizamos unha medida experimental cometemos sempre erros que producen
unha imprecisión da medida. Non hai por tanto medidas exactas. Hai medidas máis
precisas e menos precisas. Se representamos unha medida por un número todas as
cifras deben coñecerse con certeza menos a última que será dubidosa. Chamaremos
cifras significativas a todas as cifras dunha medida que se coñecen con certeza
máis a cifra dubidosa, que será a da dereita.
Analicemos estas medidas:
5,234 m: As cifras 5, 2 e 3 coñécense con certeza, a cifra
4 é dubidosa, pero todas son significativas.
12,340 m: As cifras 1,2,3 e 4 coñécense con certeza, a
cifra 0 é dubidosa, pero todas son significativas.
0,025 m: Os ceros anteriores á primeira cifra distinta de
cero non son cifras significativas. Só son cifras significativas 2 e 5.
2,5·10−2 m:
Cando un número escribímolo en notación científica todas as cifras do decimal
son significativas.
Nos datos dun problema poden aparecer as seguintes medidas: 2 m; 2,0 m; 2,00
m; 2,000 m
Non son iguais, aínda que teñan o mesmo valor.
- 2 m indica que a imprecisión da
medida é de ±1 m, e ten unha cifra significativa.
- 2,0 m indica que a imprecisión da medida é de ±0,1 m, e ten dúas cifras
significativas.
- 2,00 m indica que a imprecisión da medida é de ±0,01 m, e ten tres cifras
significativas.
- 2,000 m indica que a imprecisión da medida é de ±0,001 m, e ten catro
cifras significativas.
- Cifras significativas en operacións.
Cando realizamos operacións coa calculadora non debemos conservar todas as
cifras decimais que obtemos, pero tampouco debemos perder cifras que son
significativas. Polo que é conveniente seguir as seguintes regras:
- En sumas e restas: Súmanse ou restan as medidas e redondéase o resultado
para que teña tantas cifras decimais como o número que menos decimais teña:
2,035 m +
0,04 m + 12,9873 m = 15,0623 = 15,06 m
34,987 m -
25,46 m = 9,527 = 9,53 m
- En produtos e cocientes: Multiplícanse ou dividen as medidas e redondéase
o resultado para que teña tantas cifras significativas como o número que
menos cifras significativas teña:
2,25 m · 14693 m = 33059,25 = 33100 m2
45,38 m : 2,34 s = 19,393162 = 19,4 m/s
EXERCICIOS
PARA PRACTICAR

|
|
APARELLOS DE MEDIDA. SENSIBILIDADE E PRECISIÓN. ERROS NAS MEDIDAS |
|
Medir é comparar unha cantidade de magnitude con outra cantidade da
mesma magnitude que chamamos unidade. Para iso utilizaremos aparellos de
medida.
Unha cinta métrica, un cronómetro, un polímetro, unha báscula son aparellos
de medida.
Os aparellos de medida deben estar calibrados coas unidades que
desexamos medir. Calibrar é axustar, coa maior exactitude posible, as
indicacións dun instrumento de medida con respecto a un patrón de referencia.
Así se medimos unha distancia cunha cinta métrica, graduada en centímetros,
necesitamos que os centímetros da cinta teñan a maior exactitude posible, para
que a medida sexa boa.
- Características dos instrumentos ou aparellos de medida:
- Precisión
- Sensibilidade
- Exactitude
- Rapidez
- Fidelidade
- Rango
Precisión
É o valor máis pequeno da magnitude que se pode medir por medio dun
instrumento de medida. Por exemplo un reloxo analóxico coa agulla horaria e a
agulla minuteiro dános unha precisión dun minuto, pero un cronómetro dixital
pódenos dar unha precisión dunha décima de segundo, por exemplo. A precisión
representámola con ese valor mínimo precedido do signo máis-menos, no primeiro
caso ± 1 min, no segundo caso ± 0,1s.
Sensibilidade
É a capacidade dun instrumento de medida para apreciar cambios na magnitude
que se mide, de forma que son máis sensibles os que detectan cambios máis
pequenos da magnitude medida.
Unha regra graduada en milímetros é máis sensible que unha cinta métrica
graduada en centímetros, por exemplo.
Exactitude
É a capacidade que ten un instrumento de medida para achegarse máis ao valor
real da magnitude que se está medindo.
Rapidez
É a capacidade dun instrumento de medida para realizar a mediada no menor
tempo posible. Permitiranos realizar medidas de fenómenos que ocorren en
intervalos moi curtos de tempo.
Fidelidade
É a capacidade dun instrumento de medida para obter o mesmo valor de
magnitude tras realizar medicións sucesivas dun mesmo fenómeno nas mesmas
condicións. Canto máis parecidas sexan as medidas dun mesmo fenómeno nas mesmas
condicións máis fidel será o aparello de medida.
Rango
É o intervalo de valores que pode medir o aparello, entre a cota inferior, ou
menor valor da magnitude que se pode medir, e a cota superior, ou maior valor da
magnitude que se pode medir.
EXERCICIOS
PARA PRACTICAR
Debemos ser
conscientes que nunca poderemos realizar unha medida que nos dea un valor exacto
do que medimos. Estamos condicionados polos aparellos de medida que utilizamos.
Por exemplo, se medimos cunha cinta métrica que está graduada en centímetros
nunca poderemos conseguir unha precisión de milímetros na medida.
Se
realizamos unha única medida cometemos unha imprecisión que equivale á división
máis pequena do aparellos de medida. Fíxate sempre en cal é a división máis
pequena dos aparellos de medida que utilices.
Por exemplo,
medimos un folio cunha regra que aprecia milímetros. Obtemos un resultado de
29,7 cm. Como debemos indicar esta medida? Esta lonxitude deberiámola indicar da
seguinte forma: L = 29,7 ± 0,1 cm
0,1 cm é a imprecisión que cometemos cando
realizamos medidas cunha regra graduada en milímetros. Esta cantidade é o erro
absoluto que cometemos cando facemos esta medida.
Se facemos unha única medida o erro absoluto é
equivalente á imprecisión do aparellos de medida, ou á súa división máis
pequena.
Como nunca coñeceremos o valor exacto dunha medida
podemos achegarnos a ese valor repetindo varias veces a medida, logo calculamos
a media aritmética, e ese será o valor que tomamos como valor exacto, real, ou
máis probable.
Para unha serie de medidas, o erro absoluto é a
diferenza entre o valor obtido nunha medida e o valor exacto, calculado coa
media aritmética.
O erro absoluto será como mínimo o valor da
división máis pequena do aparello de medida.
As medidas poden ser moi diferentes, en xeral
medidas grandes terán erros absolutos grandes e medidas pequenas terán erros
absolutos pequenos. Se queremos saber o boa ou mala que é unha medida debemos
calcular o erro relativo que relaciona o erro absoluto dunha medida co valor
exacto da medida, e adóitase dar en tanto por cen. Canto menor sexa o erro
relativo mellor, de máis calidade, será a medida.
O erro relativo é o cociente en porcentaxe do
erro absoluto dunha medida e o valor exacto da medida.
EXERCICIOS
PARA PRACTICAR

|
|
ANÁLISE DE DATOS EXPERIMENTAIS. ESTIMACIÓN DO ERRO. EXPRESIÓN DE RESULTADOS |
|
Como dixemos no apartado anterior, unha forma de minimizar o erro que
cometemos cando medimos é repetir una mesma medida varias veces. Faremos así un
tratamento estatístico dos resultados.
O valor máis probable da medida será a media aritmética das medidas
realizadas.
Para poder valorar e axustar o resultado ao valor real da magnitude que
medimos, temos que facer unha estimación do erro que cometemos. O camiño máis
fácil cando non son moitas medidas é calcular o erro absoluto de cada medida
como explicamos no apartado anterior e logo facer a media aritmética de eses
erros.
Por exemplo, queremos medir o ancho do encerado cunha regra que aprecia
milímetros.
Facemos 5 medidas, con estes resultados:
A 3ª medida podemos descartala, pois se desvía moito das outras e é
claramente errónea.
O valor máis probable da medida será a media aritmética:
Redondeando a décimas de centímetro, que é a precisión da regra e por tanto o
mínimo erro que debemos ter en conta.
Agora calculamos o erro absoluto en cada medida e facemos a media aritmética
destes:
Redondeando a 1 cifra significativa.
Así, o erro que acompaña ao valor máis probable será o maior entre a
imprecisión do aparello de medida (0,1 cm) e o resultado estatístico (0,5 cm).
O resultado da medida expresarase:
No noso exemplo:
O valor real do encerado estará entre 223,5 cm e 224,5 cm.
EXERCICIOS
PARA PRACTICAR

|
|
REPRESENTACIÓN GRÁFICA. RELACIÓN LINEAL. ECUACIÓN DA RECTA REPRESENTATIVA |
|
Xa vimos, ao estudar o método científico, que ao estudar a relación entre
magnitudes podiamos chegar a atopar leis que expresabamos con ecuacións
matemáticas. Como se consegue isto?
O primeiro será determinar ben que magnitudes imos relacionar. Os fenómenos
físicos ou químicos dependen en xeral de moitas variables. Para estudalos e
atopar a relación entre estas variables debemos, nos experimentos, manter
constantes todas as variables menos dúas, que son as que imos relacionar. Supón
que ao variar dous ou máis variables varía outra, non saberemos a que variable
botar a culpa desa variación, por iso debemos fixar unhas condicións iniciais
nas que só poidan variar dúas variables. Se ao variar una a outra varía,
manténdose as demais constantes, xa sabemos que esa é a variable responsable do
cambio.
Por tanto deseñaremos os experimentos fixando que variables poden variar e
cales deben de manterse constantes.
Lembra o experimento do péndulo. Tiñamos tres variables, a masa do péndulo, a
lonxitude do péndulo e o período. Para estudar a influencia da lonxitude do
péndulo no período mantiñamos constante a masa do péndulo.
Unha vez definidas estas variables que imos estudar, modificamos unha e
observamos que valores toma a outra. Estes resultados recollémolos en táboas de
datos. As táboas irán encabezadas polas magnitudes para estudar e as unidades
que estamos a usar.
Por exemplo:
Con estas táboas xa podemos observar se hai relación entre esas magnitudes,
se ao variar una a outra tamén varía é que están relacionadas. Pero que tipo de
relación teñen? Isto non o podemos determinar coa táboa. Necesitamos representar
unha gráfica sobre uns eixos cartesianos para atopar a relación matemática entre
esas magnitudes.
Se representamos os datos da táboa anterior obtemos:
Observamos que é unha curva. Atopar a ecuación da curva que se axusta a unha
serie de puntos non é fácil. É máis fácil atopar a ecuación dunha recta que se
axuste a puntos que están suficientemente aliñados. Por tanto tentaremos atopar
sempre unha distribución de puntos que se axusten a unha recta. Para logralo
podemos facer cambios de variables que nos permitan obter unha recta. Logo
farémolo para o caso do péndulo que estamos a estudar.
A ecuación da recta ten unha forma do tipo:
y = a·x + b
onde (a) é a pendente e ( b) a ordenada na orixe. (y) é a variable dependente
e (x) a variable independente.
No noso experimento fomos dándolle valores á lonxitude do péndulo e obtivemos
uns valores do período do mesmo. A lonxitude é a variable independente e o
período a variable dependente.
Cando representamos os puntos nunha gráfica e estes están o suficientemente
aliñados, para supoñer que a relación entre as magnitudes é a ecuación dunha
recta, debuxamos a recta que mellor se axuste a esa distribución de puntos,
deixando se é necesario tantos puntos por unha banda da recta como pola outra,
xa que calquera medida virá afectada dun certo erro de forma que as medidas non
se axusten ao valor teórico que debesen ter. Lembra que estamos a traballar con
valores experimentais e todos están afectados dun certo erro.
Unha vez que temos a recta debuxada calculamos a pendente.
Volvamos ao noso experimento do péndulo. O gráfica período-lonxitude non era
unha recta. Probemos a representar T2 fronte a L.
Representamos agora T2 fronte a L.
Isto xa se axusta máis a unha recta. Observamos que é unha recta que
practicamente pasa pola orixe. Podemos calcular a pendente. Para iso utilizamos
un intervalo de dous puntos que estean sobre a recta.
Xa atopamos a ecuación que relaciona o período coa lonxitude. Esta ecuación
permítenos facer predicións, por exemplo calcular o período dun péndulo de 10 m,
ou calcular a lonxitude dun péndulo que mida segundos en cada oscilación, co que
xa temos un reloxo.
Esta ecuación, que comprobamos que nos funciona, en realidade non é válida
fisicamente, por que? Pois porque non é homoxénea, non teñen as mesmas unidades
ou dimensións as magnitudes ao carón e outro do igual. Non é homoxénea desde o
punto de vista dimensional, e todas as fórmulas físicas débeno de ser. Por iso a
análise dimensional é importante en física.
Cal é a fórmula correcta?
Esta si é homoxénea dimensionalmente. Por que entón nos funcionaba a nosa
fórmula? Pois porque o número pi e a raíz cadrada da aceleración da gravidade
teñen aproximadamente o mesmo valor. Ao traballar a unha mesma altura sobre a
superficie terrestre non observamos a influencia da gravidade da Terra. Por iso
nosa fórmula dábanos resultados válidos aínda que non sexa homoxénea.
De todos os xeitos aprendemos neste experimento a atopar a ecuación da recta
que relaciona dúas variables.
- Construír a recta de regresión cunha folla de cálculo.
En matemáticas, regresión lineal ou axuste lineal é un modelo que nos permite
atopar a recta á que se axusta unha serie de puntos o suficientemente aliñados.
Vexamos como podemos representar gráficas lineais con Calc, a folla de
cálculo de LibreOffice.
Cando relacionamos dúas variables obtemos táboas de valores. Unha será a
variable independente e outra a variable dependente. A variable que controlamos
é a variable independente, a outra será a variable dependente. Cando
relacionamos o período do péndulo coa masa, a masa é a variable independente,
pois poñemos nós as masas que queremos no péndulo, o período será a variable
dependente, xa que dependendo da masa obteremos un período determinado.
No noso exemplo chámolle X á variable independente e Y á variable dependente.
Cando facemos experimentos recollemos os valores en táboas. Como exemplo
temos esta:
Tamén podémola escribir en vertical:
Xa podemos representar esta táboa nunha gráfica usando Calc de LibreOffice.
Abrimos un libro de Calc.
Escribimos os valores nunha táboa usando as celas da folla de cálculo. Á
esquerda a variable independente e á dereita a variable dependente:
Sinalamos o rango de toda a táboa, incluído o nome das columnas.
Buscamos a icona de Gráfico, ou imos no menú para Inserir Gráfico:
Seleccionamos o tipo de gráfico: XY (dispersión): Escollemos Só
puntos:
En Elementos do Gráfico podemos dar un Título ao gráfico, nomear os eixos e
mostrar ou non a lenda. Clicamos en Finalizar.
Sobre un dos puntos, pulsamos botón dereito e escollemos Inserir liña de
tendencia.
Pulsamos en lineal, Mostrar ecuación e mostrar coeficiente de determinación R2.
Sobre os eixos, pulsamos botón dereito e podemos inserir ou non cuadrícula
principal e secundaria:
Sobre os eixos, pulsamos botón dereito, en Formato de eixos podemos
modificar: valor mínimo, valor máximo, Intervalo principal e cantidade de
intervalos secundarios.
Sobre a ecuación, pulsamos botón dereito, en Formato de ecuación de liña de
tendencia,
imos a Números, Categoría Números con dous decimais.
Vemos que aparece no gráfico a liña de tendencia, que é a recta que mellor se
axusta aos datos da gráfica.
Deben quedar tantos puntos por encima como por baixo da recta. Tamén podemos atopar puntos que se afastan moito da liña de
tendencia, nese caso poderiamos desprezar algún valor, ao supoñer que se cometeu
moito erro na súa determinación. A ecuación móstranos a pendente e a ordenada na
orixe. O coeficiente R2 indica que os datos se axustan máis a unha
recta canto máis preto da unidade estea.
A gráfica xa a podemos copiar e colocar en calquera páxina dun procesador de
texto para incluír nos nosos traballos.
EXERCICIOS
PARA PRACTICAR

|
  
|
|
