         |
|
|
|
A MATERIA |
|
En física e química imos estudar a
materia.
Que nos di o dicionario da materia? Materia
= "Realidade espacial e perceptible polos sentidos da que están feitas
as cousas que nos rodean e que, coa enerxía, constitúe o mundo físico".
Tamén nos di, "materia física diferenciada das demais por unha serie de
propiedades determinadas".
Por tanto a materia é todo o que percibimos
polos nosos sentidos, ten masa e enerxía, ocupa un espazo, e aínda que
sexa invisible para nosa vista como os gases, podémolos percibir polo
resto dos nosos sentidos.
É importante que saibas que os distintos
tipos de materia podémolos distinguir polas súas propiedades diferentes,
para distinguir estas propiedades necesitamos facer medidas. Por iso o
proceso de medida será algo importante neste tema. |
|
O MÉTODO CIENTÍFICO |
|
É o método que seguen os científicos para realizar o seu traballo, que é descubrir esas leis que se esconden no mundo que nos rodea e permítennos entendelo mellor. Con elas poderemos predicir situacións novas e buscar aplicacións tecnolóxicas que nos fagan a vida máis agradable.
Este método baséase nunha serie de etapas que haberá que seguir de forma consecutiva.
1º)
Presentación dun problema a investigar.
Os nenos pequenos unha das cousas que primeiro aprenden a dicir é por que?. Os científicos tamén. Só que estes o din durante toda a vida. E non son fáciles de convencer, parten da experiencia da realidade que lles proporciona a observación.
OBSERVACIÓN: Tratar de extraer a máxima información, a poder ser cuantitativa, do fenómeno observado.
-
Teremos que
MEDIR, para transformar as nosas observacións en datos cuantitativos.
-
Empregaremos
APARELLOS DE MEDIDA que deberán estar adecuadamente calibrados e manipulados.
-
RECOLLEITA DE
DATOS: Recolleremos toda a información complementaria que podamos, e aproveitaremos outras investigacións previas ou similares.
2º)
Dar unha explicación do problema.
Os interrogantes que xorden no apartado anterior hai que explicalos mediante diferentes hipóteses. É importante non desbotar a priori ningunha das hipóteses.
FORMULACIÓN DE HIPÓTESES: Unha hipótese é unha suposición que explica determinado fenómeno e que pode ser comprobada por vía experimental. As hipóteses poden ser válidas ou non válidas, serán válidas cando se poidan comprobar por medio de experimentos cuantitativos. As hipóteses válidas poden ser verdadeiras ou falsas, serán verdadeiras cando o resultado do experimento confirma a hipótese, se o resultado do experimento contradi a hipótese será falsa.
3º)
Comprobar experimentalmente a veracidade das hipóteses.
EXPERIMENTACIÓN: Primeiro illaremos as variables que inflúen no problema. Logo observaremos que ocorre ao manter constantes todas as variables menos dúas. Como se comporta unha cando varía a outra? Elaboraremos gráficas para indagar a relación matemática entre as variables. Con esta información verase se se verifica a hipótese ou non.
4º) Emisión de
conclusións.
Redactar o informe da investigación, coas hipóteses que se aceptan como verdadeiras. Debe recoller o proceso desde a presentación do problema ata a emisión de conclusións.
-
OBSERVA O
SEGUINTE VÍDEO:
RESPONDE ÁS
SEGUINTES CUESTIÓNS:
-
Cal é o problema a
resolver e en que observacións iniciais baséase?
-
Cantas hipóteses se
propoñen? Cales?
-
Que método se emprega
para a comprobación das hipóteses?
-
O experimento proporciona
resultados satisfactorios de acordo con algunha das hipóteses?
-
Sería posible neste caso, en
base ao método científico, extraer algunha conclusión?
EXERCICIOS
PARA PRACTICAR

|
|
APLICACIÓN
DO MÉTODO CIENTÍFICO: PRÁCTICA DO RESORTE |
|
Nada mellor para
entender o Método Científico que practicalo. Ao final do tema faremos unha
práctica para aplicar o método científico. Tentaremos descubrir a relación entre
a masa que colgamos dun resorte, ou unha goma, e o alongamento do mesmo. Isto xa
o estudou Robert Hook, contemporáneo do gran Isaac Newton, e co que non levaba
moi ben, por certo, pero non por iso deixou de ser un físico brillante.
A. OBSERVACIÓN:
Todos temos a experiencia de que ao colgar un corpo dun resorte, ou dun
elástico de goma, estes alónganse. Tamén temos a experiencia de que para un
mesmo resorte ou goma, se a masa que colga é maior o alongamento é maior, pero
diferentes resortes non teñen por que alongarse o mesmo. Imos estudar este
fenómeno e tentar chegar a algunha ecuación matemática que nolo explique.
Imos dispoñer de diferentes resortes, elásticos de goma e masas, así como de
cintas métricas para medir distancias e balanzas para medir masas.
B. FORMULACIÓN DE HIPÓTESES:
Queremos saber de que depende o alongamento dun resorte ou goma cando
colgamos diferentes masas.
Para expor as hipóteses debemos de comparar dúas variables, tentando que as
demais se manteñan constantes. As variables neste problema son: a lonxitude do
resorte, a masa que colga e a elasticidade do resorte, ou maior ou menor
facilidade para recuperar a súa forma ao ser deformado.
Posible hipótese:
“Para un mesmo resorte ou goma a lonxitude do mesmo
cando colgamos unha masa é proporcional á cantidade de masa que colga.”
C. COMPROBACIÓN EXPERIMENTAL DA HIPÓTESES:
Imos tentar demostrar a veracidade ou non da hipótese. Debemos deseñar un
experimento onde só interveñan dúas variables e as demais magnitudes mantéñanse
constantes.
Para demostrar a hipótese: Colgamos diferentes masas dun mesmo resorte de
goma, e medimos a lonxitude do resorte ao colgalas, cos datos construímos unha
táboa de valores.
| m - masa (g) |
|
|
|
|
|
|
| L - lonxitude (cm) |
|
|
|
|
|
|
Estes valores representarémolos nunha gráfica. A masa en abscisas e a
lonxitude en ordenadas. Une os puntos coa curva ou a recta que máis se
axuste aos mesmos.
a) Que forma ten esta gráfica?
b) Para unha masa cero, que lonxitude do resorte dános a gráfica? Coincide co
valor real?
c) Observando a gráfica, que é proporcional á masa que colga, a lonxitude do
resorte ou o que se alonga o mesmo?
d) Confirma isto a hipótese?
D. EXTRACCIÓN DE CONCLUSIÓNS:
e) Podemos cambiar a hipótese para que se axuste á proporcionalidade
que observamos. Por exemplo: “Para un mesmo
resorte ou goma o alongamento do mesmo cando colgamos unha masa é
proporcional á cantidade de masa que colga.”
f) Calcula a pendente da gráfica coas instrucións que che dará o teu profesor
ou profesora.
g) Atopa a ecuación matemática que relaciona as variables.
h) A pendente, ou constante de proporcionalidade, é sempre a mesma, ou
depende do resorte? Repite a experiencia con outro resorte distinto. A ecuación
que obtés é a mesma?
i) Unha ecuación matemática énos moi útil se nos permite realizar predicións.
Poderías utilizar esta ecuación para calcular unha masa problema que se colgue
do resorte?
E. ELABORACIÓN DUN INFORME:
Non esquezas elaborar un informe da túa experiencia, Contesta as preguntas
que se che formularon e redacta as dúbidas e interrogantes que se che
presentaron durante a súa realización.
USO DUNHA SIMULACIÓN
Para realizar esta práctica tamén podes utilizar esta simulación:
Experimento coa simulación: Imos traballar no apartado ESTIRAMENTO.
A) Imos usar o resorte 1. Podes facer que a forza do resorte sexa máis pequena
ou máis grande, pero non a cambies en todo o experimento, se non é coma se
cambiases de resorte.
Dispós de tres masas para colgar, de 50, 100 e 250 g. Marca no cadro da dereita,
"Lonxitude sen estirar" e "Posición de equilibrio".
Colga cada unha destas masas e mide coa regra o alongamento do resorte. Constrúe
unha táboa cos datos. Calcula a pendente da gráfica.
Atopa a ecuación que relaciona a masa co alongamento do resorte.
Tes tres masa problema, vermella, azul e verde. Colga estas masas do resorte e
calcula o valor das masas a partir da gráfica e da ecuación que atopaches.
B) Repite o experimento con outro resorte, cambia polo tanto a forza do resorte.
Obtés os mesmos valores para as masas problema?

|
|
PROCESO
DE MEDIDA |
|
Imos suscitarnos un problema:
Imaxina que todos os da clase desexamos saber o altos que somos.
Poderiamos utilizar categorías para dicir a nosa estatura: Moi altos,
altos, medianos, baixos e moi baixos. Se cada un clasifica a toda a clase
nestas categorías poida que non coincidísemos todos, pois son categorías
cualitativas, ser alto pode ser diferente segundo as persoas. Tamén
podemos facer outra cousa, clasificarnos de máis altos a máis baixos,
basta con compararnos de dous en dous e ordenarnos en fila. Poida que nalgún
caso dubidásemos, un compañeiro pode ter un peiteado máis alto que
outro, ou un calzado con máis tacón que outro. Comparar entre dúas
persoas non é difícil. No mellor dos casos chegariamos a ordenarnos por
alturas, pero non poderiamos dicir o que medimos.
Como vemos compararnos é relativamente fácil, pero só nos vale para saber
se somos máis altos ou máis baixos que outro, non podemos dar un valor desa altura. Para dar un valor necesitamos compararnos cunha altura fixa. Ocórresevos algún método para conseguilo?
Para medir necesitamos definir algunhas palabras.
A
que chamamos magnitudes en física?
MAGNITUDE: é calquer propiedade dun corpo que sexa medible, é dicir,
que se pueda cuantificar ou expresar con números.
Que
é medir unha magnitude física?
MEDIR é comparar unha cantidade dunha magnitude con outra cantidade
da mesma magnitude que se toma como patrón (ou referencia) e que se denomina UNIDADE.
Fíxaste como mide a distancia a unha barreira o árbitro nun partido? Se a barreira parécelle que está moi preto do xogador que saca a falta mide con pasos a distancia á que debe estar a barreira. Compara a distancia á que está a barreira con outra distancia, o seu paso. Cando non temos unha unidade de medida mellor un paso sácanos do apuro, é unha medida aproximada, pero sempre será mellor unha medida aproximada que ningunha medida. Recorda o verbo importante é comparar,
medir é comparar, xa sabes que.
Como
elexir unha unidade?
Cando se elixe unha unidade pénsase nunha serie de requisitos que é
convinte que cumpra, como:

|
|
SISTEMA
INTERNACIONAL DE UNIDADES |
|
Ata finais do século XIX, cada país utilizaba para medir unha mesma magnitude unha unidade diferente. Hoxe en día, a maioría dos países acepta o
SISTEMA INTERNACIONAL DE UNIDADES (S.I.)
As unidades
fundamentais do Sistema Internacional:
|
Magnitudes básicas do Sistema Internacional de Unidades |
|
MAGNITUDE |
UNIDADE |
SÍMBOLO |
| Lonxitude |
metro |
m |
| Masa |
quilogramo |
kg |
| Tempo |
segundo |
s |
| Intensidade de corrente eléctrica |
amperio |
A |
| Temperatura termodinámica |
grao Kelvin |
K |
| Cantidade de substancia |
mol |
mol |
| Intensidade luminosa |
candela |
cd |
|
DEFINICIÓNS |
| |
DEFINICIÓN
PREVIA |
DEFINICIÓN
DENDE 2019 |
| metro |
O metro é a distancia percorrida pola luz no baleiro
en
1/299.792.458 segundos. |
O metro, símbolo m, é a unidade SI de
lonxitude. Defínese ao fixar o valor numérico da velocidade da luz no
baleiro, c, en 299 792 458, cando se expresa na unidade m·s−1,
onde o segundo defínese en función da frecuencia do Cesio ΔνCs.
c = 299 792 458 m·s−1 |
| quilogramo |
Masa do quilogramo patrón internacional, que se
conserva en Sèvre, perto de Paris. |
O quilogramo, símbolo kg, é a unidade SI
de masa. Defínese ao fixar o valor numérico da constante de Planck, h, en
6,626 070 15·10−34, cando se expresa na unidade J· s, igual
a kg·m2·s−1, onde o metro e o segundo defínense
en función de c e ΔνCs. h = 6,626 070 15·10−34
J·s |
| segundo |
Duración de 9.192.631.770 períodos
da radiación do átomo de cesio-133 na transición entre dous niveis da estructura
hiperfina do seu estado fundamental. |
O segundo, símbolo s, é a unidade SI de
tempo. Defínese ao fixar o valor numérico da frecuencia da transición
hiperfina do estado fundamental non perturbado do átomo de cesio-133, ΔνCs,
en 9 192 631 770, cando se expresa na unidade Hz, igual a s−1.
ΔνCs = 9 192 631 770 s−1 |
| amperio |
Intensidade dunha corrente eléctrica constante que, cando flúe entre dous condutores paralelos de lonxitude indefinida e de sección transversal circular infinitamente pequena situados a unha distancia recíproca de 1 metro e colocados no baleiro, fai que un condutor exerza sobre o outro unha forza de
2.10-7 newtones por
cada metro. |
O amperio, símbolo A, é a unidade SI de
corrente eléctrica. Defínese ao fixar o valor numérico da carga elemental,
e, en 1,602 176 634 ·10−19, cando se expresa na unidade C, igual
a A· s, onde o segundo defínese en función de ΔνCs.
e = 1,602 176 634 ·10−19 C |
| kelvin |
Fracción 1/273,16 da temperatura termodinámica
do punto triple da auga. |
O kelvin, símbolo K, é a unidade SI de
temperatura termodinámica. Defínese ao fixar o valor numérico da constante
de Boltzmann, k, en 1,380 649 ·10−23, cando se expresa na unidade
J· K−1, igual a kg·m2·s−2·K−1,
onde o quilogramo, o metro e o segundo defínense en función de h, c e ΔνCs.
k = 1,380 649 ·10−23 J·K−1 |
| mol |
Cantidade de substancia dun sistema que
contén
tantas entidades elementais como átomos hai en 0,012 kg de carbono-12.
Débese especificar o tipo das entidades elementais, xa sexan átomos,
moléculas, ions, electróns, ou outras. |
O mol, símbolo mol, é a unidade SI de
cantidade de substancia. Un mol contén exactamente 6,022 140 76 ·1023
entidades elementais. Esta cifra é o valor numérico fixo da constante de
Avogadro, NA, cando se expresa na unidade mol−1, e
denomínase número de Avogadro.
A cantidade de substancia, símbolo n, dun sistema, é unha medida do número
de entidades elementais especificadas. Unha entidade elemental pode ser un
átomo, unha molécula, un ión, un electrón, calquera outra partícula ou grupo
especificado de partículas.
NA = 6,022 140 76 ·1023 entidades elementales. |
| candea |
Intensidade luminosa, nunha dirección dada, dunha fonte que emite unha radiación monocromática de frecuencia 540 × 1012 hercios e cuxa intensidade energética nesa dirección é 1/683 vatios por estereorradián. |
A candea, símbolo cd, é a unidade SI de
intensidade luminosa nunha dirección dada. Defínese ao fixar o valor
numérico da eficacia luminosa da radiación monocromática de frecuencia
540·1012 Hz, Kcd, en 683, cando se expresa na unidade
lm·W−1, igual a cd·sr·W−1, ou a cd· sr·kg−1·m−2·s3,
onde o quilogramo, o metro e o segundo defínense en función de h, c e ΔνCs.
Kcd = 683 lm·W−1 |
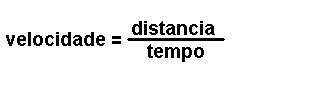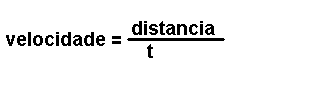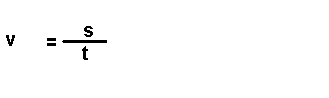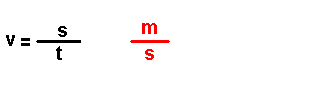
Magnitudes
derivadas.
Son magnitudes que se definen a partir das magnitudes fundamentais. Por exemplo:
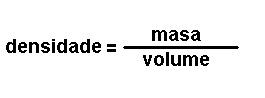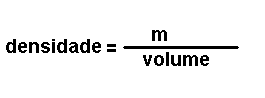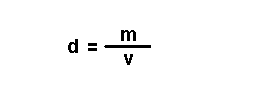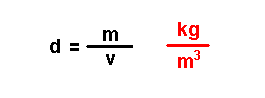
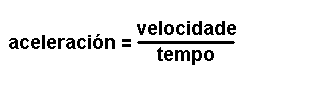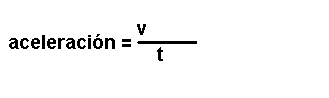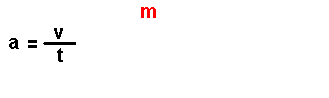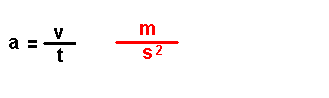
Múltiplos
e submúltiplos:
| Prefixo |
Símbolo |
Factor multiplicador |
| Tera- |
T |
1012 u |
| Xiga- |
G |
109 u |
| Mega- |
M |
106 u |
| kilo- |
k |
103 u |
| hecto- |
h |
102 u |
| deca- |
da |
10 u |
| unidade |
u |
1 u |
| deci- |
d |
10-1 u |
| centi- |
c |
10-2 u |
| mili- |
m |
10-3 u |
| micro- |
μ |
10-6 u |
| nano- |
n |
10-9 u |
| pico- |
p |
10-12 u |
O factor multiplicador é o número polo que tes que multiplicar a medida para transformala na unidade.
Por exemplo, 2 Mm = 2·106 m ou
5 nm = 5·10-9 m
EXERCICIOS
PARA PRACTICAR

|
|
TRANSFORMACIÓN
DE UNIDADES |
|
As unidades transfórmanse con facilidade a través dos factores de conversión.
Consiste en multiplicar unha medida polo cociente que nos dá a equivalencia entre a unidade que queremos substituír e a nova unidade.
Este cociente ten valor unidade, xa que o numerador é equivalente ao
denominador.
A unidade que poñemos no denominador é a que queremos eliminar, e no numerador vai a nova unidade.
Cando escribas a equivalencia entre as unidades dálle valor unidade á maior delas. Por exemplo: é máis fácil entender
1 km = 1000 m que 1 m = 0,001 km aínda que sexan as dúas igualdades válidas.
Exemplo 1: Calcula cantos km son 245 m:
A equivalencia entre (km) e (m) é: 1 km = 103 m

As medidas de superficie
mídense en m2 e os seus múltiplos e submúltiplos. Estas unidades non varían de 10 en 10 como
as unidades de
superficie, varían de 100 en 100. Por exemplo: 1m2 = 100 dm2
; 1m2 = 10000 cm2
As medidas de volume mísense en m3 e os seus múltiplos e submúltiplos. Estas unidades non varían de 10 en 10 como
as unidades de
superficie, varían de 1000 en 1000. Por exemplo: 1m3 = 1000 dm3
; 1m3 = 1000000 cm3
As medidas de capacidade
mídense en litros (L) e os seus múltiplos e submúltiplos. Pero estas unidades
tamén son equivalentes as unidades de volume:
Por exemplo: 1
m3 = 1 kL; 1 dm3 = 1 L;
1cm3 = 1 mL
O método dos factores de conversión é especialmente útil no caso das unidades derivadas, como ocorre nas unidades de velocidade ou de
densidade.
Exemplo 2: Calcula cantos m/s son 120
km/h.
A equivalencia entre
(km) e (m) é: 1 km = 103 m. E a
equivalencia entre (h) e (s) é: 1 h
= 3600 s.

Exemplo 3: Calcula cantos km/h son 40 m/s.
A equivalencia entre
(km) e (m) é: 1 km = 103 m. E a
equivalencia entre (h) e (s) é: 1 h
= 3600 s.

É importante tamén saber pasar de complexo de h:min:s a horas, e viceversa, xa que na vida diaria manexámonos en horas, minutos e segundos. Por exemplo, cando abriches esta páxina eran as:
. Que facer nestes casos?
Pasar de complexo a incomplexo: Cantas horas son 2h:25min:30s?
a) Pasa os minutos a horas, e os segundos a horas e suma: 2h:25min:30s = 2h + 25min · 1h/60min + 30s · 1h/3600s = 2,425h
b) Ou tamén, aproveitar a tecla (º ' '') de graos, minutos e segundos da calculadora, que
tamén segue o sistema sexaxesimal:
2h:25min:30s = 2 (º ' '') 25 (º ' '') 30 (º ' '') = 2,425h
Pasar de incomplexo a complexo: Cantas h:min:s son 1,755h?
a) Pasa os decimais de horas a minutos, e os decimais de minutos a segundos:
1,755h = 1h + 0,755h · 60min/1h = 1h + 45,3 min = 1h + 45min + 0,3 min · 60s/1min =1h 45min 18s
b) Ou tamén, aproveitar a tecla (º ' '') de graos, minutos e segundos da calculadora, que
tamén segue o sistema sexaxesimal:
1,755h = 1,755 (º ' '') (=) (º ' '') = 1º 45º 18 = 1h 45min 18s
EXERCICIOS
PARA PRACTICAR

|
|
MATERIAL
BÁSICO DE LABORATORIO |
|
A maioría dos materiais utilizados no laboratorio de química son de vidro por que presentan unha serie de vantaxes como ser fáciles de limpar, ser transparentes, ser bastante inertes aos reactivos químicos, e poder usarse a temperaturas relativamente altas. Fronte a esta serie de vantaxes teñen un grande inconveniente: ser moi fráxiles, polo que debes ter moito coidado cando os utilices.
|
 |
VASO DE PRECIPITADOS
É un recipiente cilíndrico con base plana, e na parte superior un pico ou beizo facilita o vertido de líquidos.
Xeralmente presenta graduación para a medida aproximada do líquido que contén, Pódense atopar de 10, 50, 100, 250, 500, 1000 e 2000 ml.
É o recipiente de uso máis frecuente e variado. Serve para trasvasar líquidos, quentalos, mesturalos, disolver sustancias, realizar reaccións químicas, e moitos máis usos. |
 |
MATRAZ ERLENMEYER
É un recipiente de forma troncocónica cunha boca na parte superior. Presenta graduación para a medida aproximada do líquido que contén. Utilízase en volumetrías pola facilidade para ser axitado sen derramar líquido. Tamén se emprega para recoller líquidos en montaxes de destilacións. |
 |
MATRAZ AFORADO
É un recipiente en forma de pera, de fondo plano e pescozo alto. Permite medir de forma exacta volumes de líquidos.
Na parte do pescozo presenta unha marca ou enrase, que indica a altura que debe alcanzar o líquido para que o matraz conteña a capacidade que indica. Os de uso máis frecuente son de 50, 100, 250, 500 e 1000 ml.
Utilízase para preparar disoluciones de concentración coñecida e na disolución de mostras nun volume determinado. |
 |
KITASATO
É un recipiente semellante ao matraz erlenmeyer cunha saída lateral próxima ao pescozo.
Emprégase para filtracións por succión, previa conexión a un sistema de baleiro (trompa de auga). Tamén se pode empregar para reaccións con produción de gases. |
 |
FUNIL
É un aparello de forma cónica que ten no extremo unha prolongación tubular para facilitar o trasvase de líquidos ou disoluciones dun matraz a outro. Tamén se emprega para filtar por gravidade colocándolle un cono de papel de filtro. |
 |
PAPEL DE FILTRO
Material necesario para as filtraciones, hainos de diferente poro. |
 |
PROBETA
É un tubo de vidro con base. Presenta graduación e emprégase para medidas de volumes. As capacidades máis frecuentes
son: 10, 25, 50, 100, 500 e 1000 ml |
 |
ESPÁTULA
Permite coller pequenas cantidades de produtos sólidos. Poden dispoñer dunha culleriña no extremo. |
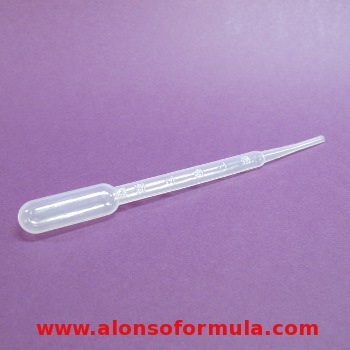 |
CONTAGOTAS OU PIPETA PASTEUR
Consiste nun tubo cun estreitamento no súa parte inferior e no seu extremo superior leva unha pera de goma para succionar o líquido e verterlo posteriormente.
Utilízase para engadir líquidos pinga a pinga. É un instrumento de medida aproximada, xa que o volume das pingas depende da natureza do líquido. |
 |
NOZ
Serve para suxeitar unha pinza a un soporte con barra. |
 |
PINZA
Serve para suxeitar os aparellos dunha montaxe. |
 |
SOPORTE CON BARRA
Empréganse para construír as diferentes montaxes. Xunto coas noces e pinzas suxeitaremos todos os aparellos da montaxe. |
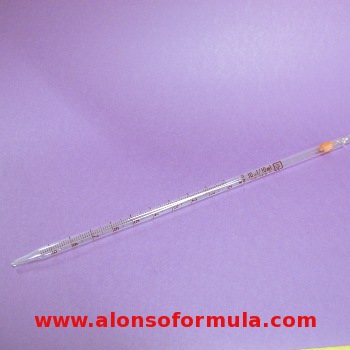 |
PIPETA GRADUADA
É un tubo de vidro de sección uniforme, cun estreitamento no súa parte inferior. Presentan unha graduación, ou escala de divisións, en 1,0 ml, 0,1 ml ou 0,01 ml dependendo da capacidade da pipeta. As súas capacidades máis frecuentes son: 5, 10, 25 e 50 ml. |
 |
ASPIRADOR
Aparello que se usa coa pipeta, actúa aspirando aire e enche a pipeta de líquido, cunha roda facilita o enrase e un orificio que ao liberalo facilita o trasvase do contido. |
 |
TERMÓMETRO DE MERCURIO
Aparello para a medida de temperaturas. A toxicidade do mercurio fai que hoxe estean sendo substituídos polos electrónicos. |
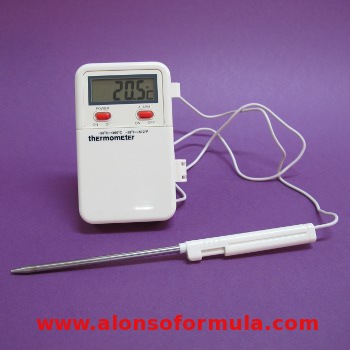 |
TERMÓMETRO ELECTRÓNICO
Úsanse cada vez máis no laboratorio. Pero como calquera aparello electrónico debe ser adecuadamente calibrado. |
 |
VARILLA DE VIDRO
Aparello utilizado para axitar líquidos e facilitar a disolución de sólidos. |
 |
FRASCO LAVADOR
Permite dispoñer de auga destilada na preparación de disoluciones. Axuda a arrastrar o soluto que queda adherido ás paredes dos recipientes. |
 |
TUBO DE ENSAIO
É un recipiente de forma cilíndrica e fondo redondo. Utilízase para realizar ensaios ou probas cualitativas de reaccións con pequenas cantidades. |
 |
LENTES DE PROTECCIÓN
Lentes de plástico que protexen ao operario de salpicaduras que de alcanzar os ollos poden ser moi perigosas. |
 |
LUVAS DE PROTECCIÓN
Luvas que protexen do contacto con produtos corrosivos e nocivos para a pel. |
 |
MECHERO BUNSEN
Mechero de butano. Aporta unha fonte puntual de calor para calentamiento de líquidos, realización de reaccións e traballo con tubo de vidro. |
 |
BALANZA ELECTRÓNICA
Balanza de uso común no laboratorio pola facilidade de manexo. Permite a tara do recipiente que usamos para pesar. |
 |
FRASCOS E ETIQUETAS
As disolución gardámolas en frascos e as etiquetamos para mellor uso das mesmas. |
 |
FORNELO ELÉCTRICO
Fonte de calor para quentamento de líquidos con axuda de recipientes como vasos de precipitados. |
EXERCICIO 1
EXERCICIO 2
EXERCICIO 3
EXERCICIO 4
|
|

|
|
ETIQUETADOS
DE PRODUCTOS: PICTOGRAMAS |
|
Moitos produtos do mercado son ou poden ser perigosos para as persoas ou o medio ambiente. A Unión Europea propón o uso de pictogramas, imaxes que se inclúen no etiquetado, para alertar desa perigosidade. Os pictogramas actuais teñen forma de rombo vermello con fondo branco e un debuxo esquemático que alerta de diferentes perigos, como podes ver no seguinte cadro:
|
PICTOGRAMAS |
| Pictograma |
Símbolo |
Significado |
Precaucións |
Exemplos |
| Nocivo
para a saúde 
|
Signo de exclamación |
Pode irritar as vías respiratorias
Pode provocar somnolencia ou vértigo
Pode provocar unha reacción alérgica na pel
Provoca irritación ocular grave
|
Evitar a respiración do produto e usar o produto en lugares ventilados e protexerse con luvas do contacto directo.
En caso de contacto coa pel: lavar con auga e xabón abundantes.
En caso de contacto cos ollos: aclarar cuidadosamente con auga durante varios minutos.
En caso de inxestión: chamar a un CENTRO de información toxicológica ou a un médico en caso de malestar. |
Deterxentes para lavadoras,
limpadores de inodoros,
líquidos refrixerantes,
amoníaco,
lixivia |
| Perigo para o medio ambiente

|
Medio ambiente |
Moi tóxico para os organismos acuáticos, con efectos nocivos duraderos.
|
Evitar a súa liberación ao medio ambiente.
Desechar estes produtos nun punto limpo ou en contenedores adecuados. |
Plaguicidas,
biocidas,
gasolina,
benceno,
cianuro de potasio |
| Inflamable

|
Chama |
Gas/Aerosol/Líquido/Sólido extremadamente inflamable
ou inflamable |
Utilizar en lugares ben ventilados.
Evitar fontes de calor cando se usen ou almacenen.
Non pulverizar sobre unha chama aberta.
Manter o recipiente pechado herméticamente.
Manter en lugar fresco.
Protexer da luz do sol. |
Hidróxeno,
etino,
éter etílico,
etanol,
acetona,
gasolina,
butano,
gas natural |
| Comburente

|
Chama sobre un círculo |
Pode provocar ou agravar un incendio ou unha explosión; comburente ou moi comburente. |
Manter afastado de fontes de calor, faíscas.
Non almacenar nin usar en contacto con produtos inflamables.
Usar con luvas/prendas/lentes/máscara de protección. |
Osíxeno,
nitrato de potasio,
peróxido de hidróxeno ou auga osixenada. |
| Corrosivo

|
Corrosión |
Provoca quemaduras graves na pel e lesións oculares graves |
Usar con elementos protectores como luvas, lentes e mascarillas.
Lavarse concienzudamente trala manipulación.
Conservar únicamente no recipiente orixinal. |
Desatascadores de tuberías,
ácido acético,
ácido clorhídrico,
hidróxido de sodio,
amoníaco |
| Explosivo

|
Bomba estoupando |
Explosivo. |
Evitar golpes.
Levar luvas/prendas/lentes/máscara de protección.
Solicitar instrucións especiais antes do uso.
Manter afastado de fontes de calor, faíscas, chama aberta ou superficies quentes.
Non fumar. |
Fogos artificiais,
produtos pirotécnicos,
munición |
| Gas a presión

|
Bombona de gas |
Contén gas a presión. |
Protexer da luz do Sol.
Pode provocar queimaduras ou lesións crioxénicas.
Levar luvas/lentes/máscara que illen do frío.
Non someter a altas temperaturas, ou achegalas a fontes de calor. |
Botellas de gas a presión,
insecticidas caseiros,
ambientadores caseiros |
| Perigo grave para a saúde

|
Perigo para a saúde |
Pode ser mortal en caso de inxestión e penetración nas vías respiratorias
Prexudica a determinados órganos
Pode provocar cancro |
En caso de inxestión: chamar inmediatamente a un CENTRO de información toxicolóxica ou a un médico.
Usar mascarillas e luvas na súa manipulación.
Lavarse concienzudamente trala manipulación. |
Metanol,
monóxido de carbono,
cloro,
trementina,
gasolina |
| Extremadamente tóxico

|
Caveira e tibias cruzadas |
Mortal en caso de inxestión
Mortal en caso de inhalación
Tóxico en caso de inxestión
Tóxico por inhalación |
Lavarse concienzudamente trala manipulación.
En caso de inxestión: chamar inmediatamente a un CENTRO de información toxicolóxica ou a un médico.
En caso de contacto coa pel: lavar suavemente con auga e xabón abundantes.
Usar medidas de seguridade adecuadas, lentes, luvas, máscaras de gas. |
Plaguicidas,
biocidas,
metanol,
cianuro,
trióxido de arsénico |
| Lembra que ningún produto con pictogramas de seguridade debe estar ao alcance dos nenos nin de persoas vulnerables. |

|
|
PROPIEDADES
XERAIS E CARACTERÍSTICAS DA MATERIA |
|
Xa vimos que as magnitudes físicas son propiedades que podemos medir ou cuantificar. Estas propiedades poden ser xerais ou características da materia. En xeral as magnitudes miden propiedades xerais da materia, é dicir, propiedades que poden ter un valor calquera nunha sustancia, por exemplo: a masa, o volume, a temperatura ou a presión. Se un anaco de metal ten unha masa ou outra nos indica o grande ou pequeno que poida ser pero non nos dá información de que metal poida ser. Serían útiles magnitudes que nos puidesen dar información de que sustancia é, iso pasa coas propiedades características. As propiedades características medímolas con magnitudes como: a densidad, a calor específica ou a resistividade. Si temos unha sustancia pura, é dicir que non sexa mestura doutras sustancias, estas propiedades características pódennos informar de que sustancia se trata. Por exemplo podemos calcular a densidad de diferentes metais para poder caracterizalos. Si a densidad calculada coincide coa dun metal determinado, probablemente trátese dese metal, pero si non coincide sabemos seguro que non se trata dese metal.

|
|
CÁLCULO
DA DENSIDADE |
|
Que é a densidade e como calcular a densidad dunha sustancia?
A historia de Arquímedes e a coroa de ouro.
Imos utilizar esta simulación da Universidade de Colorado para realizar
cálculos de densidades
En INTRODUCIÓN:
Podes calcular a densidade de distintos materiais.
Observa que se afunden máis ou menos na cubeta de auga segundo a
densidade que teñan.
En COMPARAR:
Observa o comportamento de corpos de mesma masa,
de mesmo volume e de mesma densidade fronte á auga. De que depende que
floten máis ou menos?
En MISTERIO:
Calcula a densidade dos corpos problema e pescuda
de que material pode tratarse coa táboa de densidades.
EXERCICIOS
PARA PRACTICAR

|
|
DETERMINACIÓN
EXPERIMENTAL
DA DENSIDADE |
-
Determinación da densidade dun líquido puro. Auga
Para determinar experimentalmente a densidade dun líquido
puro, como auga, debemos medir unha masa de certa cantidade de auga, e logo
medir o seu volume.
Para medir a masa usaremos a balanza de laboratorio, o
recipiente pode ser unha probeta, que tamén nos servirá para medir o seu
volume.
 |
 |
 |
| Colocamos la probeta en la balanza y taramos, para restar la
masa de la probeta |
Echamos una cierta cantidad de agua en la probeta, medimos
la masa con la balanza. |
Y medimos el volumen con la probeta. Luego calculamos la
densidad. |
Lembra anotar os valores e as unidades. Logo usarás estes
datos para calcular a densidade.
-
Determinación da densidade dunha disolución. Sal en
auga
Unha disolución de sal en auga é líquida, así que
procederemos igual que no apartado anterior. A diferenza é que nun líquido
puro sempre imos obter a mesma densidade, pero nunha disolución o valor da
densidade dependerá da súa concentración, é dicir, da proporción de sal en
auga.
 |
 |
 |
| Colocamos a probeta na balanza e taramos, para restar a masa
da probeta |
Botamos unha certa cantidade de auga salgada na probeta,
medimos a masa coa balanza. |
E medimos o volume coa probeta. Logo calculamos a densidade. |
-
Determinación da densidade dun sólido de forma
prismática ou esférica.
Se o sólido ten unha forma simple, como un prisma
cuadrangular ou unha esfera, podemos determinar o seu volume medindo as súas
dimensións cunha regra ou cun calibre, se queremos ser máis precisos.
Medir cun calibre:
Se a forma é un prisma cuadrangular, medimos as súas tres
dimensións para calcular o volume: V = a · b · c
 |
 |
 |
| Medimos a base do prisma co calibre. |
Medimos a altura do prisma co calibre. Cos datos calculamos
o volume. |
Medimos a masa coa balanza. Logo calculamos a densidade. |
Se a forma é unha esfera medimos o diámetro, para calcular o
radio, e con este calcular o volume da esfera: V = 4/3 π r3
Despois de medir a súa masa na balanza calculamos a
densidade.
-
Determinación da densidade dunha pedra por inmersión
en auga.
Cando temos un corpo de forma irregular como unha pedra é
máis complicado medir o volume.
Se o corpo é pequeno e cabe na probeta, introducimos unha
certa cantidade de auga na probeta e medímola, logo mergullamos o corpo con
coidado e medimos o volume que alcanza a auga, a diferenza destes dous
volumes dános o volume do corpo.
Se o corpo é grande, e non cabe na probeta, usamos un vaso
de plástico no que caiba, introducímolo cheo de auga noutro recipiente, ao
introducir o corpo no vaso a auga derrámase quedando no recipiente exterior.
Agora xa podemos medir este volume de auga nunha probeta, será igual ao
volume do corpo.
 |
 |
| Coa balanza medimos a masa da pedra. |
Enchemos un vaso de auga dentro dun cristalizador. |
 |
 |
| Introducimos a pedra no vaso, derramarase un volume de auga
igual ao volume da pedra. |
Botamos a auga derramada na probeta e determinamos o seu
volume. Cos datos de masa e volume calculamos a densidade. |
Para medir a masa usamos como sempre a balanza. Finalmente
calculamos a densidade.
Os densímetros son aparellos de laboratorio deseñados para
medir a densidade de diferentes líquidos. Podémolos usar para medir a
densidade de líquidos puros ou de disolucións.
Parece ser que foi
Hipatia de
Alexandría a súa inventora.
Os densímetros están fabricados de vidro dentro do cal hai
un contrapeso calibrado para que ao introducilo nun líquido, polo principio
de Arquímedes, sobresae unha escala onde podemos ler a densidade do líquido.
Hai densímetros específicos para algunhas disolucións, por
exemplo o alcoholímetro ou alcohómetro: para medir a porcentaxe de
alcol dunha bebida alcohólica, o sacarímetro: para medir a cantidade
de azucre dunha melaza, ou o lactómetro: para medir a densidade e
calidade do leite.
Déixoche este vídeo para que vexas algúns tipos e como se
usan:

|
|
|
        |
|
